
가장 긴 증가하는 부분 수열
가장 긴 증가하는 부분 수열(LIS, Longest Increasing Subsequence) 혹은 최장 증가 부분 수열은 대표적인 동적 계획법(Dynamic programming) 문제다.
아래와 같이 특정 길이의 수열 A가 주어졌을 때 가장 긴 증가하는 부분 수열의 길이를 찾는 것이 문제이다. 아래 예시에서는 {10, 20, 30, 50}의 부분 수열이 수열 A의 가장 긴 증가하는 부분 수열이고 길이는 4이다.
A = {10, 20, 30, 15, 25, 50}
가장 긴 증가하는 부분 수열 문제는 간단한 O(N^2)의 알고리즘과 조금 복잡한 O(N log N) 두 가지 알고리즘으로 해결 가능하다.
O(N^2) 알고리즘
동적 계획법에서는 어떻게 값을 재사용하는가를 결정하는 것이 핵심 아이디어다. 즉, 이전에 계산했던 값을 활용해 미래의 값을 계산할 것이기 때문에 어떤 값을 계산해 저장하고 있을지를 결정해야 한다. 그리고 가장 긴 증가하는 부분 수열문제에서는 배열의 i 번째 값으로 끝나는 가장 긴 증가하는 부분 수열의 길이를 dp[i] 배열에 저장한다.
dp[i]: A[i]로 끝나는 가장 긴 증가하는 부분 수열의 길이
즉 dp에 저장되는 값을 표로 그려보면 아래와 같다. 편의를 위해 A의 원소가 인덱스 1부터 시작된다고 가정하겠다.

A[1]로 끝나는 가장 긴 증가하는 부분 수열은 {10} 뿐이고 이 수열의 길이는 1이다.
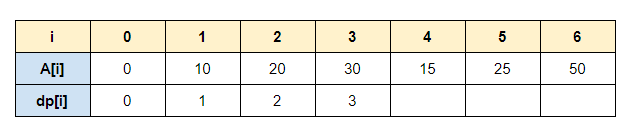
마찬가지로 계속 진행했을 때 A[3]으로 끝나는 가장 긴 증가하는 부분 수열은 {10, 20, 30}이고 이 수열의 길이는 3이다.

이때 A[4]의 경우 A[4]로 끝나는 가장 긴 증가하는 부분 수열은 {10, 15} 이기 때문에 dp[4]의 값은 2가 된다. A[5]의 경우 A[5]로 끝나는 가장 긴 증가하는 부분 수열은 {10, 20, 25} 그리고 {10, 15, 25} 이렇게 각각 2개가 존재한다. 두 가지 경우 모두 길이는 3이기 때문에 dp[5]의 값은 3이 된다.

위와 같은 방법으로 계산하면 마지막 dp[6]의 값은 4가 된다. 그리고 주어진 A 수열에서 가장 긴 증가하는 부분 수열의 길이는 dp 값 중 최댓값인 4가 된다. 이때 중요한 아이디어는 dp[i] 값을 볼 때 이전 값인 dp[0] ~ dp[i-1]까지의 값을 참고한다는 것이다. 즉 dp[i]는 0 ~ i-1까지 인덱스를 가지는 원소 중 값은 A[i] 보다 작으면서 가장 큰 dp 값을 가지는 원소에 1을 더한 값이다. 간단하게 적으면 아래와 같다.
dp[i]: (A[i]보다 작은 A[j] (0<=j<=i-1) 중 가장 큰 dp[j] 값) + 1
코드는 아래와 같다.
# 가장 긴 증가하는 부분 수열 - 백준 11053
# O(N^2)
import sys
N = int(input())
# 수열 A
A = [0]
# A[i]로 끝나는 가장 긴 증가하는 부분 수열의 길이
dp = [0] * (N+5)
A += list(map(int, sys.stdin.readline().strip().split()))
for i in range(1, N+1): # 1 ~ N
for j in range(i): # 0 ~ i-1
# dp[i]는 A[i] 보다 작은 A[j] 중 가장 큰 dp[j] 값에 1을 더한 값이다.
if A[i] > A[j]:
dp[i] = max(dp[j]+1, dp[i])
print(max(dp))
''' Result
Input
6
10 20 10 30 20 50
Output
4
'''
O(N log N) 알고리즘
위 알고리즘은 간단하지만 비효율적이다. dp[i] 값을 계산하기 위해 dp[0] ~ dp[i-1]를 다 확인을 해야 하기 때문이다. 따라서 O(N^2)의 시간 복잡도를 가지는데 이를 O(N log N)으로 줄일 수 있는 방법이 있다. 현재 dp[i]를 갱신하는데 걸리는 시간 복잡도가 O(N)인데 이를 이진 탐색(Binary Search)을 활용해 O(log N)으로 줄이는 방법이다. 하지만 현재 dp는 정렬되어있지 않기 때문에 이진 탐색을 사용할 수 없는데, dp를 아래와 같이 정의하면 이진 탐색을 활용해 시간을 줄일 수 있다.
dp[i]: 길이가 i 인 증가하는 부분 수열 중 끝점의 최솟값
사실 위와 같이 dp를 정의한 이유는 동일한 길이의 증가하는 부분 수열의 경우 끝점이 작은 것이 더 효율적이기 때문이다. 즉 아래와 같은 동일한 길이의 두 증가하는 부분 수열이 있을 때 30이 이 수열에 끝에 추가되면 A는 30과 연결될 수 없지만 B는 끝점이 25이기 때문에 30과 연결될 수 있다. 따라서 증가하는 부분 수열의 길이가 동일한 경우 끝점이 작은 것을 고르는 것이 더 좋다.
A={10, 20, 30} B={10, 20, 25}
dp를 위와 같이 정의했을 때 값의 변화를 살펴보면 아래와 같다.

i가 1일 때 길이가 1인 가장 긴 증가하는 부분 수열은 {10}뿐이고 따라서 끝점의 최솟값은 10이 된다. 또한 i가 3이 될 때까지 A[i]는 계속 증가하기 때문에 dp 배열에 값이 계속 추가된다.

하지만 i가 4가 되는 경우 기존에 있던 길이 2인 증가하는 부분 수열 {10, 20} 뿐만 아니라 {10, 15}도 가능하게 된다. 이 경우 끝점의 최솟값은 15이기 때문에 dp[2]의 값은 15로 변경되게 된다.

위와 같은 방법으로 계산했을 때 i가 5일 때와 6일 때 dp 값의 변화는 아래와 같다.


그리고 dp 배열의 길이가 가장 긴 증가하는 부분 수열의 길이가 된다.(사실 길이-1) 그리고 dp는 항상 오름차순으로 유지되기 때문에 이진 탐색을 활용할 수 있고 탐색 시간이 O(log N)으로 줄어든다. 결과적으로 dp를 갱신시키기 위해 이진 탐색을 활용해 dp[n] < A[i] <= dp[n+1] 지점을 찾고 dp[n+1]을 A[i]로 갱신한다. 그런 위치가 없을 경우 dp 배열의 끝에 A[i]를 추가한다.
[dp를 갱신시키는 방법]
- dp[n] < A[i] <= dp[n+1]을 만족하는 n이 존재할 경우 dp[n+1] = A[i]
- 없을 경우 dp 배열의 끝에 A[i] 추가
코드는 아래와 같다.
# 가장 긴 증가하는 부분 수열 2 - 백준 12015
# O(N log N)
import sys
def binarySearch(arr, left, right, value):
mid = (left + right) // 2
if left > right:
return -1
if arr[mid] < value <= arr[mid+1]:
return mid+1
if arr[mid] >= value:
return binarySearch(arr, left, mid-1, value)
if arr[mid] < value:
return binarySearch(arr, mid+1, right, value)
if __name__ == "__main__":
N = int(input())
# 수열 A
A = [0]
# 길이가 i 인 증가하는 부분 수열 중 끝점의 최솟값
dp = [0] * (N+5)
dpLength = 1 # dp 배열의 현재 길이
A += list(map(int, sys.stdin.readline().strip().split()))
for i in range(1, N+1): # 1 ~ N
index = binarySearch(dp, 0, dpLength-1, A[i])
# dp에 값이 새로 추가되는 경우
if index == -1:
dp[dpLength] = A[i]
dpLength += 1
# 끝점의 최솟값을 바꾸는 경우
else:
dp[index] = A[i]
print(dpLength-1)
''' Result
Input
6
10 20 10 30 20 50
Output
4
'''관련 문제
'개인공부 > 코테 및 알고리즘' 카테고리의 다른 글
| 코딩테스트 준비할 때 필수 개념! <완전탐색> 알아보기 (4) | 2020.12.14 |
|---|---|
| 코딩테스트 준비할 때 필수 개념! <기본 자료구조> 알아보기 (0) | 2020.12.10 |
| 코딩테스트 준비할 때 필수 개념! <문자열 처리> 알아보기 (2) | 2020.12.07 |



댓글